Searching
Objective
: To find out the
location of any given element in array. If element found then successful,
otherwise unsuccessful.
Two approaches –
1.Linear Search
(Sequential Search): if array elements in random order
2.Binary Search: if
array elements in sorted order
Linear
Search
Algorithm: Let a is given array and
no. of elements is n. Pos is representing the position of desired element k in array a, if element found
otherwise, set Pos to -1. Variable i
is used as simple variable in loop.
Analysis
of Linear Search
Binary
Search
Ø Best searching approach
Constraint:
§ Given array
should be in sorted order
OR
§ First sort the
given array and then perform search, but then sorting time will be added
Binary
Search (Iterative)
Algorithm: Let a is given array which is sorted in ascending order
and no. of elements is n. Pos is representing the position of desired element Item in array a, if
element found otherwise, set Pos to -1. Variable mid is used to keep the mid
index of array.
1.Initialize low =0,
high = n-1
2.While low <= high
3. mid =
(low+high)/2
4. If a[mid] == Item
5. Set Pos = mid
6. Break and Jump to step 10
7. Else if Item < a[mid]
8. high = mid -1
9. Else low
=mid +1
10.If Pos < 0
11. Print “Element is not found”
12.Else Print Pos
Binary
Search Illustration
Binary
Search (Iterative)
Analysis
of Iterative Binary Search
Binary
Search (Recursive)
Algorithm Bin_Search(a, Item,low, high): Let a is given array
which is sorted in ascending order and no. of elements is n. Pos is
representing the position of desired element Item in array a, if element found otherwise, set Pos to -1.
Variable mid is used to keep the mid index of array. Here, initially low and
high are assigned the lowest and highest index of array a.
1.If low<=high
2. mid =
(low+high)/2
3. If a[mid] == Item
4. Set Pos = mid
5. Return Pos
6. Else if Item < a[mid]
7. Return
Bin_Search(a,Item,low,mid-1)
8. Else Return
Bin_Search(a,Item,mid+1,high)
9.Return Pos
Problem
For the code segment
below estimate the time-complexity in the big-oh notation.
for (int i=0; i< n; i++)
for (int j=0; j*j <n;j++)
for (int k=0; k < n/2;k++)
print (i+j+k);
Soln:
Loop 1 rate of change depends linearly on n -> O(n)
-- Linear
Loop 2 rate of change depends on the squared root of n
-> O(n^0.5) -- Fractional power
Loop 3 rate of change depends linearly on n/2, but 1/2
constant can be removed -> O(n/2) -- Linear
So, the overall complexity would be O(n) * O (n^0.5) * O
(n) = O (n^2.5)
Complexity
analysis of an algorithm
Two main methods:
1.Direct
counting:Time complexity will be sum of the individual steps
(primitive Operations)
Best for repeated iterations (loops).
2.
Recurrence equation(Recurrence Relations):
an equality or inequality describing the function in
terms of its behavior on smaller
inputs.
Best for recursive functions and structures.
Recurrence
Relation
Base Case:
When
you write a recurrence relation you must write two equations:
one
for the general case and
one
for the base case.
These
correspond to the recursive function to which the recurrence applies. The base
case is often an O(1) operation,
though it can be otherwise.
In
some recurrence relations the base case involves input of size one, so we
wrote
T(1) = O(1).
However, there are cases
when the base case has size zero. In such cases the base could would be
T(0) = O(1).
Solving Recurrence Relations
T(n) = 2 T(n/2) + O(n) // [the O(n) is for Combine]
T(1) = O(1) // Base Case
We'll write n instead of O(n) in the first line below because it makes the
algebra much simpler.
T(n) = 2 T(n/2) + n
= 2 [2 T(n/4) + n/2] + n
= 4 T(n/4) + 2n
= 4 [2 T(n/8) + n/4] + 2n
= 8 T(n/8) + 3n
=16 T(n/16) + 4n
…..
…..
= 2k T(n/2k)
+ k n
We know that T(1) = 1 and this is a way to end
the derivation above.
In particular we want T(1) to appear on the
right hand side of the = sign.
This means we want:
n/2k = 1 OR n = 2k OR log2 n
= k
Continuing with the previous derivation we get the
following since k = log2 n:
= 2k T(n/2k)
+ k n
= 2log2 n T(1) + (log2n) n = n + n log2 n
= O(n log n)
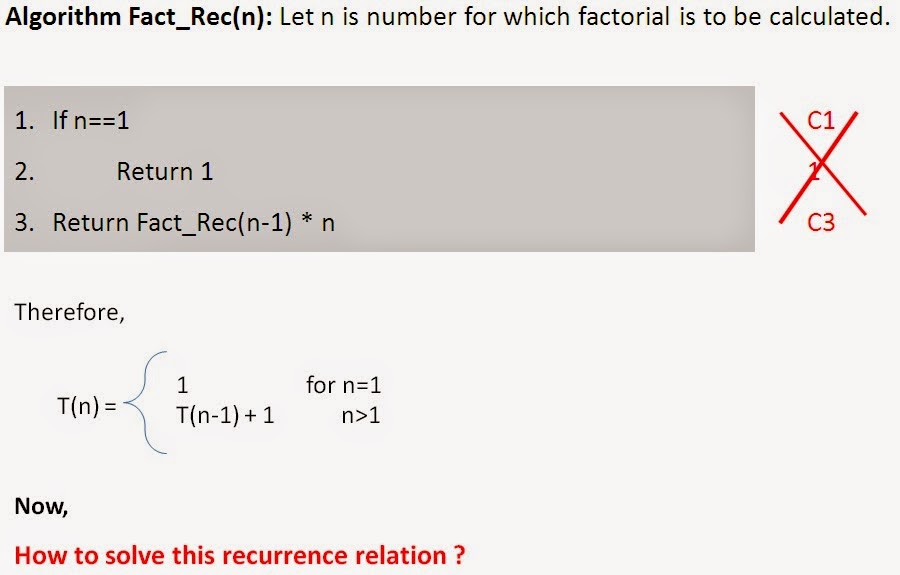
Illustration
1: Factorial Recursive
Substitution method – try to find the
pattern
While the equation certainly expresses the complexity
function, a non-recursive (or closed-form) version would be more
useful.
T(1) = 1
T(n) = T(n -1) + 1
T(n) = T(n -1) + 1 //T(n
- 1) = T(n - 2) + 1
= T(n - 2) + 1 + 1
= T(n - 2) + 2 //T(n
- 2) = T(n - 3) + 1
= T(n - 3) + 1 + 2
= T(n - 3) + 3 //T(n
- 3) = T(n - 4) + 1
= T(n - 4) + 4
= : : :
= T(n - k) + k
If we set n-k=1=> k=n-1 we have:
T(n) = T(1) + n-1
= 1+n-1
T(n)= n
Hence, Time
complexity = O(n)
Illustration
2: Fibonacci Recursive
This the case of Deep recursion where if the function makes
more than one call to itself, you have a deep recursion, that takes exponential
time.
Ø It grows like exponential tree.
Time complexity = O(2n)
Analysis
of Binary Search Recursive
T(n) = T(n/2) + 1
= T(n/2*2) + 1 +
1
= T(n/2*2*2) + 3
= T(n/24)
+ 4
…………….
= T(n/2k)
+ k
Let n/2k = 1, n = 2k , log2n = k * log22
i.e. k = log2n
Now,
T(n) = T(1) + log2n = 1 + log2n
= O(log2n)
Recurrence
Relations to Remember











A huge influx of slots in the casino industry | drmcd
ReplyDeleteMore than a dozen 원주 출장마사지 new slot 안동 출장샵 machines and table games are now on casino 남원 출장마사지 floors in 용인 출장샵 Las Vegas, 화성 출장샵 but the casinos already have a